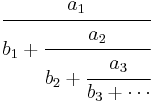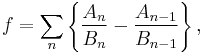Śleszyński–Pringsheim theorem

In mathematics, the Śleszyński–Pringsheim theorem is a statement about convergence of certain continued fractions. It was discovered by Ivan Śleszyński[1] and Alfred Pringsheim[2] in the late 19th century.[3]

It states that if an, bn, for n = 1, 2, 3, ... are real numbers and |bn| ≥ |an| + 1 for all n, then

\cfrac{a_1}{b_1%2B\cfrac{a_2}{b_2%2B\cfrac{a_3}{b_3%2B \cdots}}}

converges absolutely to a number ƒ satisfying 0 < |ƒ| < 1,[4] meaning that the series

f = \sum_n \left\{ \frac{A_n}{B_n} - \frac{A_{n-1}}{B_{n-1}}\right\},

where An / Bn are the convergents of the continued fraction, converges absolutely.

See also

Notes and references

  1. ^ Слешинскій, И. В. (1889). "Дополненiе къ замѣткѣ о сходимости непрерывныхъ дробей" (in Russian). Матем. сб. 14 (3): 436–438. http://mi.mathnet.ru/msb7210. 
  2. ^ Pringsheim, A. (1898). "Ueber die Convergenz unendlicher Kettenbrüche" (in German). Münch. Ber. 28: 295–324. JFM 29.0178.02. 
  3. ^ W.J.Thron has found evidence that Pringsheim was aware of the work of Śleszyński before he published his article; see Thron, W. J. (1992). "Should the Pringsheim criterion be renamed the Śleszyński criterion?". Comm. Anal. Theory Contin. Fractions 1: 13–20. MR1192192. 
  4. ^ Lorentzen, L.; Waadeland, H. (2008). Continued Fractions: Convergence theory. Atlantic Press. p. 129.